如何理解引力波效应？《张朝阳的物理课》推导测地偏离方程

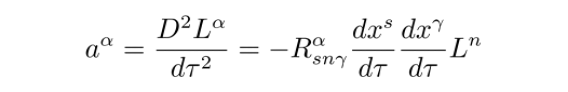
这实际上就是所谓的潮汐加速度。从方程可知，加速度由黎曼曲率张量决定。由于在牛顿力学中也存在潮汐加速度，因此在弱场慢速近似下，我们可以合理地认为二者应当一致。

另一方面，我们已经 较为熟悉克氏符，但对黎曼曲率张量相对较陌生。因此，在理解这一物理过程时，我们希望避免直接引入黎曼曲率张量。从测地偏离方程的物理意义出发，该方程描述的是两个相距很近且沿测地线运动的粒子之间的相对加速度方程。因此，我们可以直接从测地线方程出发，通过相减的方式推导测地偏离方程，而不必借助较为抽象的微分几何方法。

从测地偏离方程推导形变张量的加速度形式

在弱引力场的条件下，度规可以分解为闵氏度规及其上的微扰

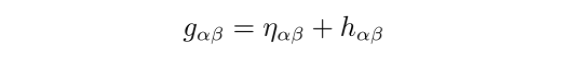
微扰部分可视为引力波带来的影响。在洛伦茨规范条件下，引力波满足波动方程：

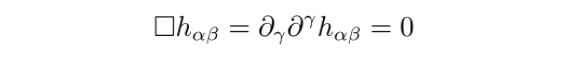
这表明引力波以光速传播。该波动方程的平面波解形式为：

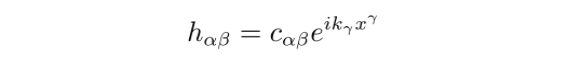
其中，波矢k取为

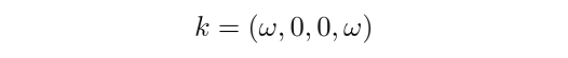
即引力波沿 z 轴传播。此时，引力波的相位可表示为：

在此，我们采用闵氏度规η升降指标。同时，坐标分量定义为：

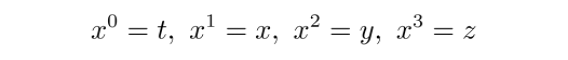
两个走测地线的粒子之间的距离是一个一阶张量

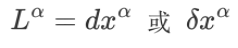
则测地线偏离方程写为

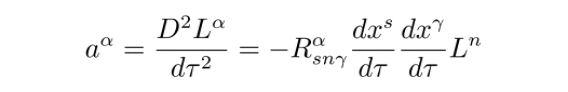
要注意的是这里的D是协变微分，而不是普通微分。在弱场低速的情况下，原时的变化dτ其实可约等于坐标时的变化dt，但我们仍旧保留dτ的写法，上面等式可简写为

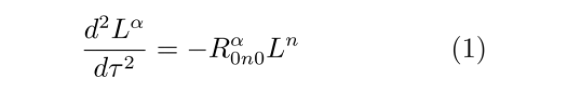
在此情况下，黎曼曲率张量可写为

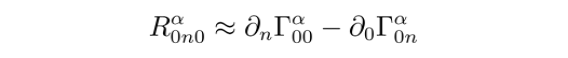
我们将微扰度规带入到克氏符中

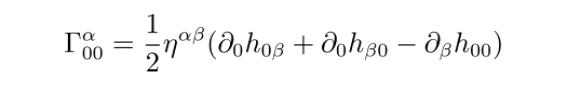
由于微扰h是纯空间张量，也就是说只要带0指标的分量都等于0，也就是

将它代入到等式(1)中，得到

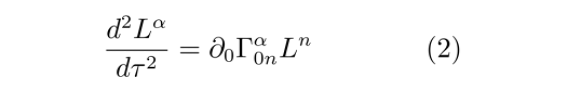
这就是形变矢量在弱场慢速极限下所满足的方程。此结果经过简化后不再显式涉及黎曼曲率张量，从而避免了微分几何的复杂性。

张朝阳从测地偏离方程推导形变张量的加速度形式

从测地线推导测地偏离方程——零结果

等式(2)是从测地线偏离方程得到的，我们接下来想从测地线方程的角度获得相同的结论。

测地线方程为

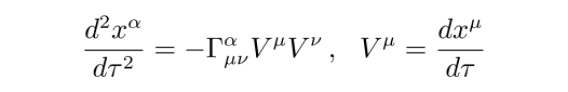
在弱场低速情况下，四维速度中除了μ=0分量外，其余分量都很小，可以忽略不计：

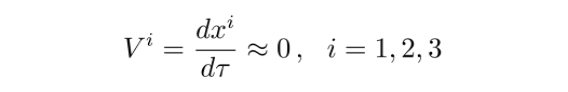
因此，V可以写为：

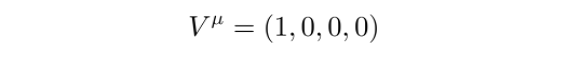
这样，测地线方程右侧求和后的16项中，只有1项非零：

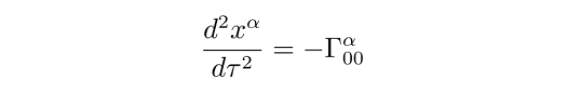
根据上面的计算，我们知道这个克氏符等于 0：

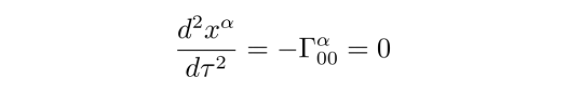
相邻粒子之间的距离差满足：

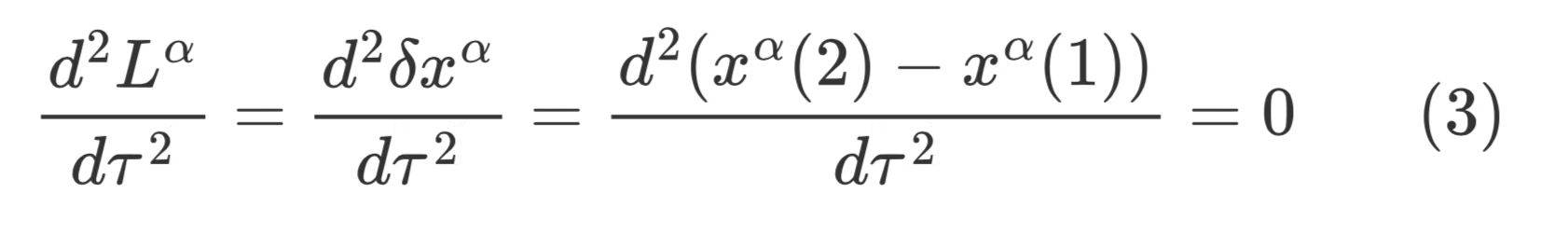
这与上面得到的等式(2)的结果不一致，因此必然存在某些概念上的问题。

张朝阳从测地线错误推导测地偏离方程

从测地线推导测地偏离方程——协变形式

上面我们看到的问题实际上源自概念上的偏差。形变矢量 L是一个一阶张量，在计算其加速度时，必须使用协变导数。这实际上意味着，对坐标的微分包含两个部分：对坐标的直接微分，以及标架基矢变化引起的附加项。这是因为引力波通过时，时空已不再是平直的。因此，这部分必然涉及克氏符，其表达式为

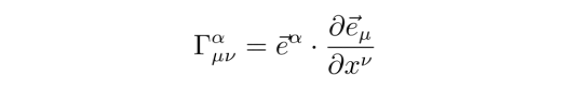
即，标架的变化所带来的贡献。

根据上面的测地线方程，有

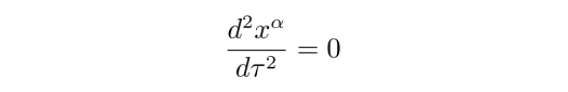
取其在两条相邻测地线上的差值，得到

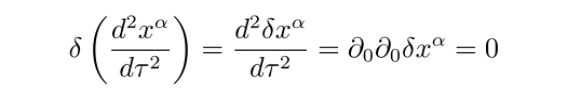
即

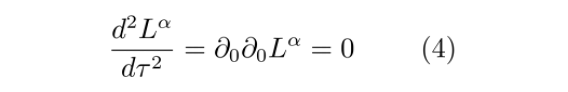
协变导数与普通导数的关系为

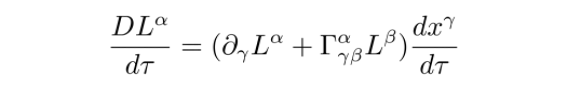
根据前述结果，四维速度为

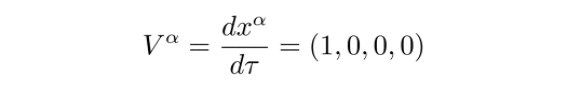
因此，有

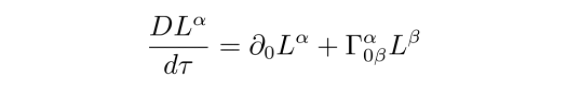
对该协变导数再求一次协变导数，得到

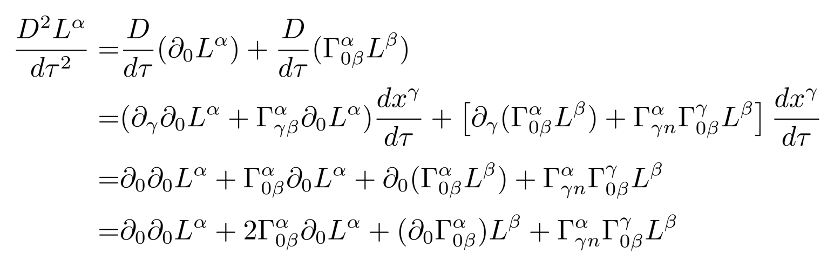
由等式 (4) 可知，第一项为零。对于第二项，有

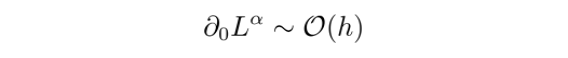
因为粒子之间的运动速度是由引力波引起的，因此其大小必定与h同阶。此外，

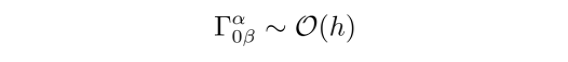
所以

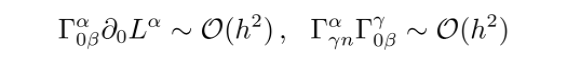
这两个项均为二阶小量，因此可以忽略。于是，

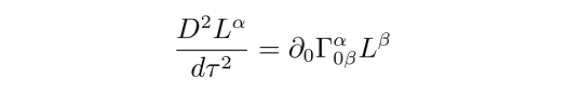
在弱场低速情况下，有

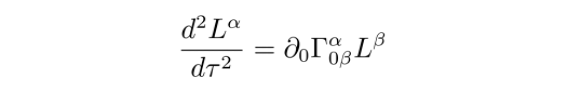
将哑指标β换成n，得

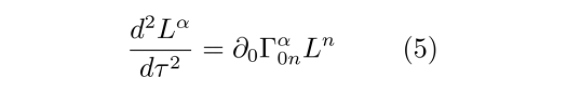
这与弱场低速下的测地偏离方程 (2) 一致。

综上所述，研究测地偏离时，必须使用协变导数，而非普通导数。

张朝阳从测地线正确推导测地偏离方程

引力波下的测地偏离

我们进一步研究方程(5)，将克氏符具体写出：

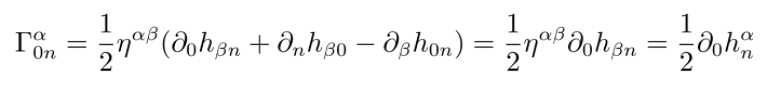
代入等式(5)，得到

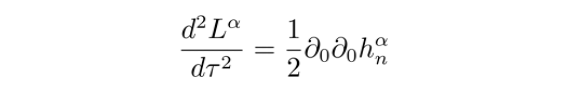
在弱场低速近似下，原时dτ近似等于坐标时dt ，因此

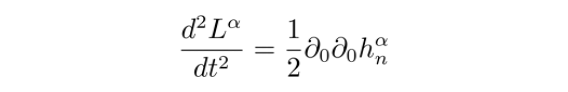
其中，引力波满足

由于引力波沿 z轴传播，形变矢量L仅在α=1,2时非零。将引力波形式代入上式，得到

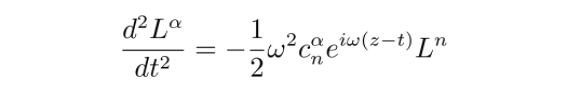
接下来，我们分别讨论以下两种情况：

这些情况的具体分析已在上次物理课中讨论过，详细内容可参考上一节的文稿或直播。

据了解，《张朝阳的物理课》于每周周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。